
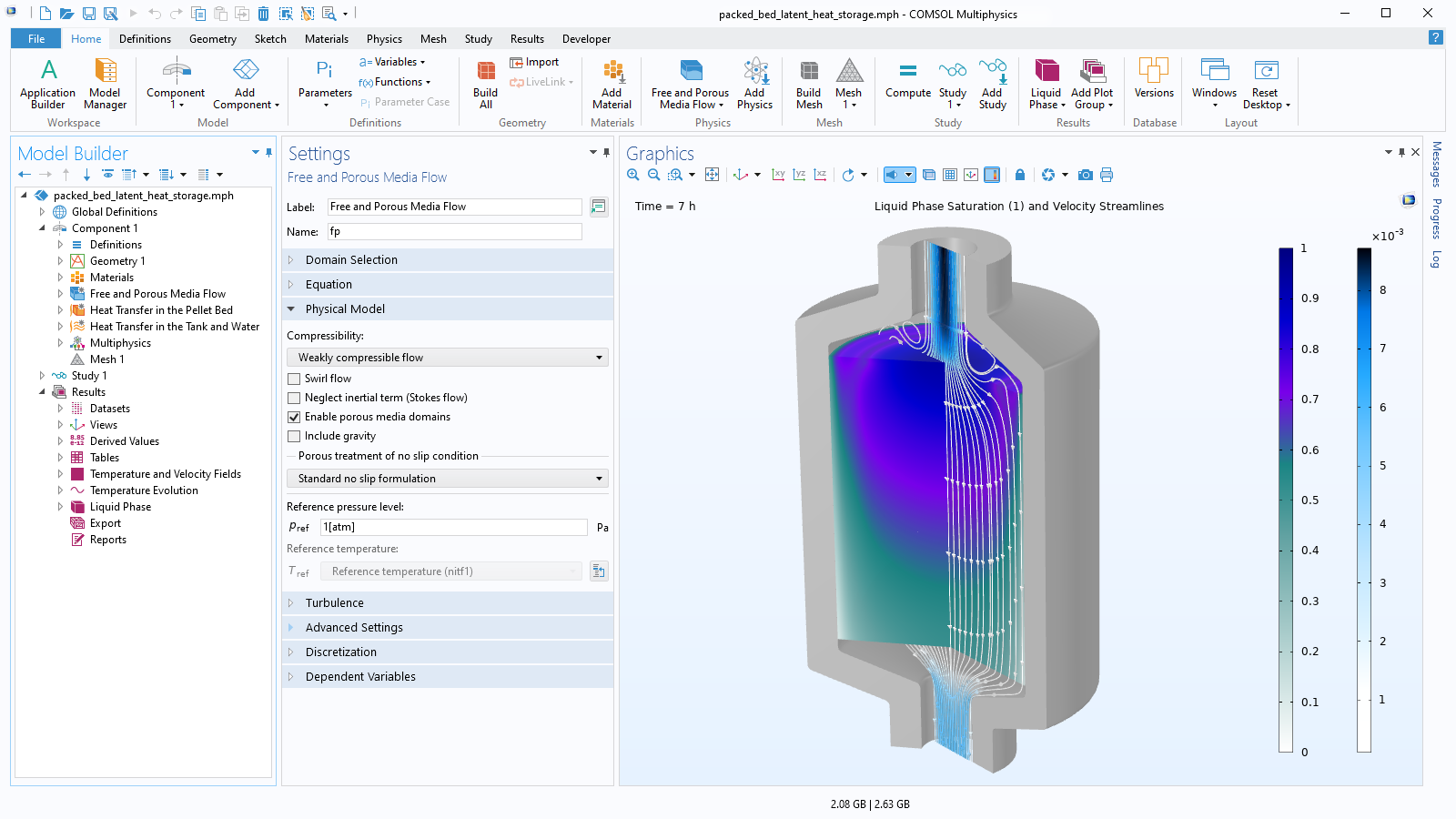

The gray nodes as removed for the serendipity elements. The black, white, and gray nodes are all present in the Lagrangian elements. Visualization of node placement in second-order elements. If a mesh can be created that is dominated by rectangular, prismatic, pyramidal, or hexahedral elements it is usually worth using the serendipity discretization, if it is available within the physics. Although the serendipity element has fewer nodes per element, it often exhibits quite good accuracy for the same mesh but a lower computational cost compared to the Lagrange element. The Lagrange element introduces additional nodes (degrees of freedom) within the elements as visualized in the figure below. This setting has an effect only if rectangular, prismatic, pyramidal, or hexahedral elements are present in the mesh. There are sometimes additionally the options of of Lagrange and serendipity elements for the quadratic and higher discretizations. Note that increasing the element order is one approach to validating your model but that you will likely want to study refining the mesh instead, as described in Performing a Mesh Refinement Study. Increasing the discretization, without changing the number of elements, will lead to a more accurate solution but will require greater computational resources. Lowering the discretization, without changing the number of elements, will lead to a model that requires less computational resources but will have lower accuracy. Based upon the particular modeling situation, changing the discretization may be motivated, and it is possible to change the discretization for each different physics interface independently, but doing so has several consequences. Problems involving fluid flow and transport are generally by default using a first-order, linear, discretization. The default discretization in many cases is second-order (quadratic), and this is partially because many of the partial differential equations have a dominant second derivative term. The discretization settings exist within each physics interface. That is, each physics interface has its own unique discretization settings that govern what order shape functions are using for those dependent variables, as shown in the example screenshot below for the Electric Currents physics interface. Plots of linear, quadratic, and cubic shape functions within a one-dimensional element.ĭifferent physics interfaces can use different sets of shape functions. The solution within the elements is based upon a linear sum of these shape functions. In the image below, the set of linear (first-order), quadratic (second-order), and cubic (third-order) shape functions are plotted.

For example, in the simplest case of a one-dimensional finite element model, the shape functions within each element are simply a set of polynomials defined over the domain.
The equations within each element are also known as shape functions and can be of different order. The solution to these equations approximates the true solution to the partial differential equation. The solution is computed by assembling and solving a set of equations over all of the elements of the model. The finite element method works by discretizing the modeling domains into smaller, simpler, domains called elements. Temperature variations are primarily in the main flow direction.Most physics interfaces within COMSOL Multiphysics use the finite element method to solve the underlying partial differential equations. Motion, hence mixing, in the transverse direction is possible, and Unmixed because the fins prevent motion in a direction ( With one fluid mixed and the other unmixed]Īlternatively, the fluids may be in cross flow (perpendicular toĮach other), as shown by the finned and unfinned tubular heatĬonfigurations differ according to whether the fluid moving over the Opposite ends, flow in opposite directions, and leave at opposite InĮnter at the same end, flow in the same direction, and leave at the One for which the hot and cold fluids move in the same or oppositeĭirections in a concentric tube (or double-pipe) construction. Heat exchangers are typically classified according to flowĪrrangement and type of construction. There are thus three heat transferįrom fluid to the inner wall of the tube, Viewed as a tube with one fluid running through it and another fluidįlowing by on the outside. The basic component of a heat exchanger can be The general function of a heat exchanger is to transfer heat from 3 Efficiency of a Counterflow Heat Exchanger 1 Simplified Counterflow Heat Exchanger (With Uniform Wall Temperature) Generalized Conduction and Previous: 18.4 Modeling Complex Physical Contents Index


 0 kommentar(er)
0 kommentar(er)
